I am using the Jane Street Real-Time Market Data Forecasting to practice and learn more about time-series forecasting. All features are anonymized and we have to predict the value of the responder_6 variable.
From previous competition I already know that the model’s forecast performance tends to decline over time. To mitigate this, we should implement a mechanism that allows us to re-train the model with the most recent data.
Another issue related to the Jane Street challenge is that the final solution must provide a response for one data batch within a 1-minute time limit. This implies that, to implement online learning, we need to re-train the model and make predictions as quickly as possible. Based on this requirement, I chose the ARIMA model to create a proof of concept.
ARIMA
ARIMA is a statistical model used for analyzing and forecasting time series data. It combines three components:
Moving Average (MA): This component incorporates the dependency between an observation and a residual error from a moving average model applied to lagged observations.
AutoRegressive (AR): This component uses the dependent relationship between an observation and some number of lagged observations.
Integrated (I): This represents the differencing of raw observations to allow the time series to become stationary.
It is all we need to proceed to the code part. When using statsmodel package, every component has a parameter counterpart in the model object: p for autoregressive, q for moving average and d for integrated.
Implementing ARIMA Online Learning
I tried to keep code organized using classes. I began by creating an ArimaTrainer.
Arima Trainer
class ArimaTrainer():
def __init__(
self,
train_size: int, # in days
data: pd.DataFrame = None,
):
"""
Initialize the ArimaTrainer class with training size and data.
Args:
train_size (int): Number of days to be used for training.
data (pd.DataFrame, optional): DataFrame containing the data to be used. Defaults to None.
"""
self.train_size = train_size
self.data = data
self.unique_dates = []
def get_last_n_dates_per_symbol(self, data: pd.DataFrame, train_size: int) -> pd.DataFrame:
"""
Load data from a DataFrame and return the last n dates for each symbol_id
Args:
data: Pandas DataFrame with training data
train_size: Number of distinct dates to keep per symbol
Returns:
pd.DataFrame: Filtered DataFrame with last n dates per symbol
"""
# Get unique dates per symbol
unique_dates = data[['symbol_id', 'date_id']].drop_duplicates()
# Sort by symbol_id and date_id in descending order, then group and take top N dates
top_dates = (
unique_dates
.sort_values(by=['symbol_id', 'date_id'], ascending=[True, False])
.groupby('symbol_id')
.head(train_size)
)
# Filter original data using these dates
final_result = (
data
.merge(top_dates, on=['symbol_id', 'date_id'], how='inner')
.sort_values(by=['symbol_id', 'date_id', 'time_id'])
[['date_id', 'time_id', 'symbol_id', 'responder_6', 'weight']]
)
# Validate that each symbol has exactly train_size distinct dates
date_counts = final_result.groupby("symbol_id")['date_id'].nunique().reset_index(name='distinct_date_count')
assert (date_counts['distinct_date_count'] == train_size).all(), (
f"Not all symbols have exactly {train_size} distinct dates. "
f"Found counts: {date_counts[date_counts['distinct_date_count'] != train_size]}"
)
return final_result
def _train_and_predict(self, s):
"""
Train an ARIMA model for a given symbol and make predictions.
Args:
s: Symbol identifier for which the model is trained.
Returns:
tuple: A tuple containing arrays of symbols and predictions.
"""
print(f'Starting training of the symbol {s}\n')
df_train = self.data.loc[
self.data['symbol_id'] == s
]
if len(df_train) > 0:
df_train = self.get_last_n_dates_per_symbol(df_train, self.train_size).reset_index(drop=True)
model = ARIMA(df_train['responder_6'], order=(1, 0, 0))
model_fit = model.fit()
# After date_id 677 the time units per day stabilizes in 968
y_pred = model_fit.forecast(steps=968).astype(np.float32).to_numpy()
symbol = np.full(len(y_pred), s)
else:
y_pred = np.full(968, 0.0).astype(np.float32)
symbol = np.full(len(y_pred), s)
return symbol, y_pred
def run(self):
"""
Execute the ARIMA training and prediction process for all symbols.
Returns:
tuple: Two concatenated arrays containing symbols and predictions.
"""
unique_symbols = self.data['symbol_id'].unique()
# Use multiprocessing to parallelize the computation
with multiprocessing.Pool() as pool:
results = list(pool.map(self._train_and_predict, unique_symbols))
# Unpack the results into two separate lists
symbol, pred = zip(*results)
symbol = np.concatenate(symbol)
pred = np.concatenate(pred)
return symbol, pred
Initialization
To instantiate the class, I expect the training window size in days and the data itself.
get_last_n_dates_per_symbol
This method is straightforward. It returns a filtered DataFrame with the last N dates for each symbol. The goal is to use this data to train the ARIMA model.
_train_and_predict
This method filter the data by one specific symbol_id, trains a ARIMA model and predict an entire day (968 time units) for the given symbol. It also accounts for new symbols, where there is no training data available, and returns a constant as the prediction in such cases.
The model = ARIMA(df_train['responder_6'], order=(1, 0, 0)) is where the model object is instantiated. The order parameter receives the p, d, and q parameters respectively (Remember: p for autoregressive, q for moving average and d for integrated.)
_train_and_predict
This method uses the previous methods to train and return predictions for all symbols. I use multiprocessing to speed up the entire process. For this reason, I chose to work with pandas DataFrame instead of polars DataFrame, as the latter seems to have an incompatibility with the multiprocessing library, causing CPU usage to drop to 0% and getting stuck processing.
Jane Predictor
This class is designed to handle data received from the submission API. It is based on the sample submission code.
class JanePredictor():
def __init__(
self,
initial_data: pl.DataFrame,
train_size: int
):
"""
Initializes the JanePredictor class with initial data and training size.
Parameters:
initial_data (pl.DataFrame): The initial dataset to be used for predictions.
train_size (int): The size of the training dataset.
Attributes:
lags_ (None): Placeholder for lag data.
cached_test_data (pl.DataFrame): Stores the initial data for caching purposes.
train_size (int): Stores the size of the training data.
"""
self.lags_ = None
self.cached_test_data = initial_data
self.train_size = train_size
def predict(self, test: pl.DataFrame, lags: pl.DataFrame | None) -> pl.DataFrame | pd.DataFrame:
"""
Predicts future values based on the test data and optional lag data.
Parameters:
test (pl.DataFrame): The test dataset containing new observations.
lags (pl.DataFrame | None): Optional lagged data to enhance prediction accuracy.
Returns:
pl.DataFrame | pd.DataFrame: A DataFrame containing predictions with 'row_id' and 'responder_6' columns.
Raises:
TypeError: If the returned predictions are not a DataFrame.
Notes:
- Aligns column types between cached data and lag data.
- Joins lag data with cached test data to fill missing values.
- Uses an ARIMA model to generate predictions.
- Ensures that the output DataFrame has the same number of rows as the input test data.
"""
if lags is not None:
# Cast columns to a common data type if necessary
self.cached_test_data = self.cached_test_data.with_columns([
pl.col("date_id").cast(pl.Int32),
pl.col("time_id").cast(pl.Int32),
pl.col("symbol_id").cast(pl.Int32)
])
lags = lags.with_columns([
pl.col("date_id").cast(pl.Int32),
pl.col("time_id").cast(pl.Int32),
pl.col("symbol_id").cast(pl.Int32)
])
lags = lags.with_columns(
(pl.col('date_id') - 1).alias('date_id')
).select(['date_id','time_id','symbol_id','responder_6_lag_1'])
self.cached_test_data = self.cached_test_data.join(
lags,
on=['date_id','time_id','symbol_id'],
how='left'
)
self.cached_test_data = self.cached_test_data.with_columns(
pl.when((pl.col("responder_6") == 0.0) & (pl.col('responder_6_lag_1') != 0.0))
.then(pl.col('responder_6_lag_1'))
.otherwise(pl.col('responder_6'))
.alias("responder_6")
).drop(['responder_6_lag_1'])
trainer = ArimaTrainer(
train_size=self.train_size,
data=self.cached_test_data.to_pandas(),
)
symbol, pred = trainer.run()
self.symbol_arr = np.array(symbol)
self.pred_arr = np.array(pred)
# Get unique symbols and their first occurrences
_, first_indices = np.unique(self.symbol_arr, return_index=True)
symbol = self.symbol_arr[first_indices]
pred = self.pred_arr[first_indices]
self.symbol_arr = np.delete(self.symbol_arr, first_indices)
self.pred_arr = np.delete(self.pred_arr, first_indices)
pred_df = pl.DataFrame({
'symbol_id': symbol,
'responder_6': pred
},
schema={
'symbol_id': pl.Int8,
'responder_6': pl.Float32
}
)
self.cached_test_data = pl.concat([
self.cached_test_data,
test.with_columns(
pl.lit(0.0).cast(pl.Float32).alias('responder_6')
).select(['date_id','time_id','symbol_id','responder_6','weight'])
],how='vertical_relaxed')
predictions = test.join(pred_df, on=['symbol_id'], how='left').select(['row_id','responder_6'])
if isinstance(predictions, pl.DataFrame):
assert predictions.columns == ['row_id', 'responder_6']
elif isinstance(predictions, pd.DataFrame):
assert (predictions.columns == ['row_id', 'responder_6']).all()
else:
raise TypeError('The predict function must return a DataFrame')
# Confirm has as many rows as the test data.
assert len(predictions) == len(test)
print(predictions.head())
return predictionsFrom this notebook we understood that new data is served by time_id. In other words, we receive a batch related from time_id = 0 and must return the predictions for this batch. According to the competition host, the lags parameter will be provided every time time_id = 0. Therefore, whenever the lags are not null, we can assume it is a new date_id. Based on this information, I chose to train the ARIMA model each time we encounter a new date_id.
The main idea is to train an ARIMA model for each symbol_id whenever we have a new date_id. We predict an entire day (968 time units) for every symbol and store these predictions in the Jane Predictor object. Then, for every prediction call that doesn’t have lags (meaning we are still within the same already predicted date_id), we retrieve the first prediction for each symbol from our Jane Predictor’s symbol_arr and pred_arr, remove it from the Jane Predictor’s attributes, join it with the test DataFrame, and return it as the prediction. In other words, symbol_arr and pred_arr function like a stack that we consume with each new time_id until we reach a new date_id.
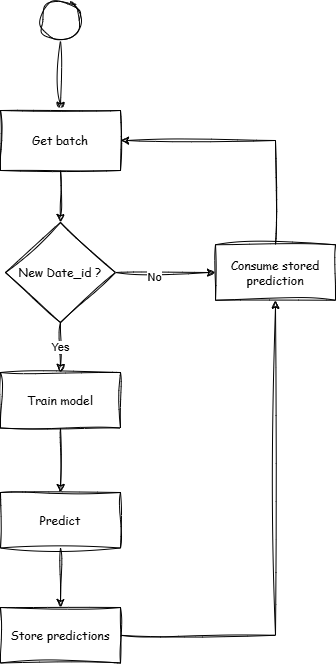
Using everything together
The code below integrates all components to enable our online learning process.
file_path = '/kaggle/input/jsrtmdf-feature-engineering/train.parquet'
train_size = 21
data = get_last_n_dates_per_symbol(file_path, train_size)
jane_predictor = JanePredictor(
initial_data = data,
train_size = train_size
)
inference_server = kaggle_evaluation.jane_street_inference_server.JSInferenceServer(jane_predictor.predict)
if os.getenv('KAGGLE_IS_COMPETITION_RERUN'):
inference_server.serve()
else:
inference_server.run_local_gateway(
(
'/kaggle/input/jane-street-real-time-market-data-forecasting/test.parquet',
'/kaggle/input/jane-street-real-time-market-data-forecasting/lags.parquet',
)
)Conclusion
We successfully created a proof of concept for online learning. By using multiprocessing, we were able to train and predict within the time limit. As future work, we can expand this concept to other models, such as LGBM.
With ARIMA, we are only using the responder_6 variable to predict itself, which means we are discarding any potential exogenous variables that could enhance the prediction process. However, we cannot use all available features to train the model due to the time constraints and the large volume of data. I believe the key to succeeding in this challenge is to select a subset of features to train a more powerful model using the online learning approach.
You can access the full code here.
I hope you enjoy!!
